Mi desempeño durante el bimestre mejoró a comparación del primer bimestre porque me pude dar cuenta que pude desarrollarme por mi misma usando excell pienso que aprender a usar estos programas es importante ya que facilita la representación de lo que son las matemáticas aunque en mi caso me hace falta la práctica a la hora de derivar o transformar una ecuación para después plasmarlo con los métodos que vimos durante el bimestre.Necesito más práctica también para hacer las tablas con diferentes métodos y además reconocerlos. Los medios que utilizamos para trabajar facilitaron todo trabajo hacen que trabajemos de una forma más rápida y si sabemos utilizarlos nos va a ir mejor y pienso que eso si se me facilita.
miércoles, 15 de mayo de 2013
¿Cómo trazar una curva paramétrica y una polar con geogebra ?
GeoGebra opera con dos tipos de curvas, paramétricas o implícitas.
Curvas Paramétricas
De formulación a(t) = (f(t), g(t)) siendo t el parámetro real dentro de cierto rango, pueden crearse usando el Comando Curva.- Estas curvas pueden...
- vincularse a comandos como Tangente o Punto y, en GeoGebra 4.2 a Comando Interseca
- complementarse con empleo de herramientas como
 Nuevo Punto y Tangente para , por ejemplo, trazar una tangente por un punto de la curva
Nuevo Punto y Tangente para , por ejemplo, trazar una tangente por un punto de la curva - asociarse a expresiones aritméticas o funciones predefinidas. Por ejemplo,
c(3)brinda el punto de posición paramétrica 3 en la curva c. - tantearse. Al tratar con extremos, digamos a y b, dinámicos se puede apelar también a deslizadores variables.Nota: Ver la
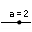 herramienta Deslizador.
herramienta Deslizador.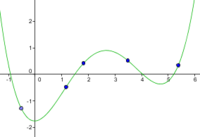
POLARES
Para graficar en coordenadas polares con GeoGebra se procede de la siguiente forma:
Sabemos que la sintaxis para graficar un punto en este programa es (x, y), bien pues para poner un punto en coordenadas polares r, theta la sintaxis es (r; theta); aquí emplearemos punto y coma para que se trate de coordenadas polares.
Ahora, si quieres dibujar el plano polar escribiremos el siguiente código:
Primero:
Secuencia[Circunferencia[(0,0), i], i,1,10]
Esto crea una secuencia o familia de círculos de centro en el origen con un incremento de 1 y con 10 círculos en total (esto lo puedes variar).
Segundo:
Secuencia[Recta[(0,0),(cos(i),sin(i))],i,0,2pi,pi/6]
Esto crea una familia de rectas que pasan por el origen con un incremento en el ángulo de inclinación de pi/6
Con esto ya tienes tu plano polar, ahora para dibujar curvas polares vamos a tener que parametrizar las funciones de la siguiente manera:
Primero ingresamos la función; por ejemplo r(x)=cos(2*x), la graficamos y luego la ocultamos (donde dice mostrar objeto), a continuación escribimos el siguiente código:
Curva[r(t)*cos(t), r(t)*sin(t), t, 0, 2pi]
y ya con esto tienes la grafica de una curva polar.
Y esta es la forma, o por lo menos una de las formas, de trabajar con gráficas y curvas en el plano polar con GeoGebra.
Sabemos que la sintaxis para graficar un punto en este programa es (x, y), bien pues para poner un punto en coordenadas polares r, theta la sintaxis es (r; theta); aquí emplearemos punto y coma para que se trate de coordenadas polares.
Ahora, si quieres dibujar el plano polar escribiremos el siguiente código:
Primero:
Secuencia[Circunferencia[(0,0), i], i,1,10]
Esto crea una secuencia o familia de círculos de centro en el origen con un incremento de 1 y con 10 círculos en total (esto lo puedes variar).
Segundo:
Secuencia[Recta[(0,0),(cos(i),sin(i))],i,0,2pi,pi/6]
Esto crea una familia de rectas que pasan por el origen con un incremento en el ángulo de inclinación de pi/6
Con esto ya tienes tu plano polar, ahora para dibujar curvas polares vamos a tener que parametrizar las funciones de la siguiente manera:
Primero ingresamos la función; por ejemplo r(x)=cos(2*x), la graficamos y luego la ocultamos (donde dice mostrar objeto), a continuación escribimos el siguiente código:
Curva[r(t)*cos(t), r(t)*sin(t), t, 0, 2pi]
y ya con esto tienes la grafica de una curva polar.
Y esta es la forma, o por lo menos una de las formas, de trabajar con gráficas y curvas en el plano polar con GeoGebra.
¿Cómo convertir una curva paramétrica y polar a una rectangular o cartesiana?
POLARES
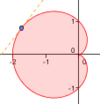
Es un sistema de coordendas bidimensional en el cual cada punto del plano se determina por un ángulo y una distancia.
De manera más precisa, se toman: un punto O del plano, al que se le llama origen o polo, y una recta dirigida (o rayo, o segmento OL) que pasa por O, llamada eje polar (equivalente al eje x del sistema cartesiano), como sistema de referencia. Con este sistema de referencia y una unidad de medida métrica (para poder asignar distancias entre cada par de puntos del plano), todo punto P del plano corresponde a un par ordenado (r, θ) donde r es la distancia de P al origen y θ es el ángulo formado entre el eje polar y la recta dirigida OP que va de O a P. El valor θ crece en sentido antihorario y decrece en sentido horario. La distancia r (r ≥ 0) se conoce como la «coordenada radial» o «radio vector», mientras que el ángulo es la «coordenada angular» o «ángulo polar».
En el caso del origen , O, el valor de r es cero, pero el valor de θ es indefinido. En ocasiones se adopta la convención de representar el origen por (0,0º).
En el plano de ejes xy con centro de coordenadas en el punto O se puede definir un sistema de coordenadas polares de un punto M del plano, definidas por la distancia r al centro de coordenadas, y el ángulo  del vector de posición sobre el eje x. Conversión de coordenadas polares a rectangulares
del vector de posición sobre el eje x. Conversión de coordenadas polares a rectangulares
 del vector de posición sobre el eje x. Conversión de coordenadas polares a rectangulares
del vector de posición sobre el eje x. Conversión de coordenadas polares a rectangulares
Definido un punto en coordenadas polares por su ángulo  sobre el eje x, y su distancia r al centro de coordenadas, se tiene:
sobre el eje x, y su distancia r al centro de coordenadas, se tiene:
 sobre el eje x, y su distancia r al centro de coordenadas, se tiene:
sobre el eje x, y su distancia r al centro de coordenadas, se tiene: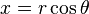
- Conversión de coordenadas rectangulares a polares

Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que la coordenada polar r es:
 (aplicando el Teorema de Pitágoras)
(aplicando el Teorema de Pitágoras)
Para determinar la coordenada angular θ, se deben distinguir dos casos:
- Para
 = 0, el ángulo θ puede tomar cualquier valor real.
= 0, el ángulo θ puede tomar cualquier valor real. - Para
 ≠ 0, para obtener un único valor de θ, debe limitarse a un intervalo de tamaño 2π. Por convención, los intervalos utilizados son [0, 2π) y (−π, π].
≠ 0, para obtener un único valor de θ, debe limitarse a un intervalo de tamaño 2π. Por convención, los intervalos utilizados son [0, 2π) y (−π, π].
Para obtener θ en el intervalo [0, 2π), se deben usar las siguientes fórmulas ( denota la inversa de la función tangente):
denota la inversa de la función tangente):
 denota la inversa de la función tangente):
denota la inversa de la función tangente):
Para obtener θ en el intervalo (−π, π], se deben usar las siguientes fórmulas:
o equivalentemente
Muchos lenguajes de programación modernos evitan tener que almacenar el signo del numerador y del denominador gracias a la implementación de la función
atan2, que tiene argumentos separados para el numerador y el denominador. En los lenguajes que permiten argumentos opcionales, la función atan puede recibir como parámetro la coordenada x.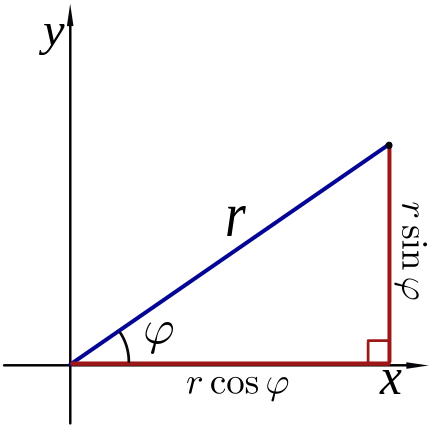
PARAMÉTRICAS
Hallar la gráfica de la ecuación cartesiana y dominio de las funciones dadas por sus ecuaciones paramétricas. Indicar el movimiento.
a) con
con ![t \in{[0,1]}](http://rinconmatematico.com/foros/Sources/latexrender/pictures/ab6924ca9e79534eb4146f981c696073.png)
b)![\begin{Bmatrix} x(t)= 2\sen^2{t}& \mbox{ }& \\y(t)=2\cos^2{t} & \mbox{}&\end{matrix}
t \in {[0,2 \pi]}](http://rinconmatematico.com/foros/Sources/latexrender/pictures/adc2650906ed94c99b33901de11118cf.png)
c)![\begin{Bmatrix} x(t)= -cos{t}& \mbox{ }& \\y(t)=sen{t} & \mbox{}&\end{matrix}
t \in{[\displaystyle\frac{ \pi}{2},\displaystyle\frac{3}{2} \pi]}](http://rinconmatematico.com/foros/Sources/latexrender/pictures/08e952f998e796a6a02ef5288e059bf8.png)
Encontrar un representación parametrica de:
a)
b)
a)
 con
con ![t \in{[0,1]}](http://rinconmatematico.com/foros/Sources/latexrender/pictures/ab6924ca9e79534eb4146f981c696073.png)
b)
![\begin{Bmatrix} x(t)= 2\sen^2{t}& \mbox{ }& \\y(t)=2\cos^2{t} & \mbox{}&\end{matrix}
t \in {[0,2 \pi]}](http://rinconmatematico.com/foros/Sources/latexrender/pictures/adc2650906ed94c99b33901de11118cf.png)
c)
![\begin{Bmatrix} x(t)= -cos{t}& \mbox{ }& \\y(t)=sen{t} & \mbox{}&\end{matrix}
t \in{[\displaystyle\frac{ \pi}{2},\displaystyle\frac{3}{2} \pi]}](http://rinconmatematico.com/foros/Sources/latexrender/pictures/08e952f998e796a6a02ef5288e059bf8.png)
Encontrar un representación parametrica de:
a)

b)

Un cambio útil suele ser:
(*):Si es una función (con el debido abuso de notación), entonces siempre se puede parametrizar a la curva como
es una función (con el debido abuso de notación), entonces siempre se puede parametrizar a la curva como 
(**):A demás, hay que aprender a reconocer curvas. Por ejemplo, las circunferencias centradas en el origen con radio siempre son de la forma
siempre son de la forma  con
con  ,
,  .
.
Usando lo anterior, los dos incisos (a), el segundo (b) y casi el (c).
Por ejemplo, para el primer (a) se tiene: llamando , se cumple
, se cumple  y luego esto se sustituye en
y luego esto se sustituye en  .
.
El segundo (a) es lo mismo usando directamente el cambio (*)
El segundo (b) también es aplicación directa del cambio (**).
(*):Si
 es una función (con el debido abuso de notación), entonces siempre se puede parametrizar a la curva como
es una función (con el debido abuso de notación), entonces siempre se puede parametrizar a la curva como 
(**):A demás, hay que aprender a reconocer curvas. Por ejemplo, las circunferencias centradas en el origen con radio
 siempre son de la forma
siempre son de la forma  con
con  ,
,  .
.Usando lo anterior, los dos incisos (a), el segundo (b) y casi el (c).
Por ejemplo, para el primer (a) se tiene: llamando
 , se cumple
, se cumple  y luego esto se sustituye en
y luego esto se sustituye en  .
.El segundo (a) es lo mismo usando directamente el cambio (*)
El segundo (b) también es aplicación directa del cambio (**).
martes, 14 de mayo de 2013
Curvas paramétricas y polares
CURVAS PARAMÉTRICAS Y POLARES
CURVAS PARAMÉTRICAS
Ecuaciones paramétricas de algunas curvas y su representación gráfica
En general, una curva plana se define por dos variables, a saber, x e y. Tal plano se conoce como plano Cartesiano y su ecuación se llama ecuación Cartesiana.
Las ecuaciones paramétricas son aquellas definidas en términos de un solo parámetro, generalmente, este parámetro es ‘t’.
Una curva que represente tal ecuación es llamada curva paramétrica. Para ello, las variables de la ecuación Cartesiana son transformadas con el fin de representar el parámetro ‘t’ como,
x = f(t) y = g(t)
Por ejemplo, una ecuación que represente la caída de una partícula desde una altura x en un tiempo t, se representa generalmente a través de una ecuación Cartesiana, sin embargo esta puede ser presentada a través de una ecuación paramétrica que sea función del tiempo t.
La curva paramétrica es el conjunto de todos los puntos de t que a su vez representan un par (x, y) o (f (t), g (t)).
Trazar una curva paramétrica es ligeramente diferente a trazar una curva plana.
Una curva paramétrica puede ser dibujada de muchas formas diferentes y la más conveniente entre ellas es la selección de ciertos valores de t y obtener los valores correspondientes de f(t) y g(t), es decir, x e y. Entonces estos son después trazados en coordenadas Cartesianas.
Sin embargo, existen problemas importantes asociados con este método, siendo uno que no conocemos los límites del parámetro. Y en ausencia de límite la gráfica se extendería en ambas direcciones hasta el infinito.
En efecto, no existe una solución adecuada a este problema, ya que todo depende completamente del problema dado y la única solución es limitarla uno mismo hasta un valor específico y asumir que esta es la extensión del gráfico.
Otro método para graficar una curva paramétrica es eliminar el parámetro de la ecuación y reducir la ecuación en términos de una ecuación Cartesiana, la cual puede ser graficada con mayor facilidad. De hecho existen varios métodos para hacer esto.
Uno de estos métodos consiste en resolver una de las ecuaciones paramétricas para la variableparamétrica ‘t’.
Reemplace este valor de ‘t’ en la otra ecuación paramétrica y déjela así, esta es una ecuación Cartesiana en términos de x e y.
Sin embargo la técnica anterior no es siempre fructífera, especialmente cuando se trata de funciones trigonométricas, ya que puede convertirla ecuación a una forma más críptica que definitivamente no pueda ser resuelta.
Hacer uso de las identidades trigonométricas definitivamente sería una mejor opción en este escenario.
Asimismo existe una amplia gama de técnicas disponibles, todo dependerá de la función dada, esto seentenderá con más práctica.
Ahora tratemos de resolver un ejemplo que involucre las técnicas descritas anteriormente para arrojar algo de luz sobre los conceptos tratados.
p = 4cos (t) q = 3 sin (t) 0 <= t <= 2
La función dada implica funciones trigonométricas así que tratemos de hacer uso de las identidades trigonométricas para reducirla. p/ 5 = cos (t) q/ 3 = sin (t)
p2/ 25 = cos2 (t) q2/ 9 = sin2 (t)
Podemos hacer uso de la identidad sin2 (t) + cos2 (t) = 1. Entonces,sume las dos ecuaciones para producir una ecuación única como,
p2/ 25 + q2/ 9 = 25cos2 (t)/ 25 + 9sin2 (t)/ 9
p2/ 25 + q2/ 9 = 1
EJEMPLO
• La curva de ecuaciones paramétricas ![[Graphics:../Images/aplicaciones_integral_gr_271.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_271.gif) para
para ![[Graphics:../Images/aplicaciones_integral_gr_272.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_272.gif) es una elipse de centro
es una elipse de centro ![[Graphics:../Images/aplicaciones_integral_gr_273.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_273.gif) y semiejes de longitudes
y semiejes de longitudes ![[Graphics:../Images/aplicaciones_integral_gr_274.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_274.gif) . Cuando
. Cuando ![[Graphics:../Images/aplicaciones_integral_gr_275.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_275.gif) se trata de una círcunferencia.
se trata de una círcunferencia.
![[Graphics:../Images/aplicaciones_integral_gr_277.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_277.gif)
![[Graphics:../Images/aplicaciones_integral_gr_276.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_276.gif)
![[Graphics:../Images/aplicaciones_integral_gr_277.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_277.gif)
- La curva de ecuaciones paramétricas
![[Graphics:../Images/aplicaciones_integral_gr_278.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_278.gif) para
para ![[Graphics:../Images/aplicaciones_integral_gr_279.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_279.gif) es la cicloide. Es la curva que describiría una chincheta clavada en una rueda de radio
es la cicloide. Es la curva que describiría una chincheta clavada en una rueda de radio ![[Graphics:../Images/aplicaciones_integral_gr_280.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_280.gif) que avanza girando sin deslizar.
que avanza girando sin deslizar.
![[Graphics:../Images/aplicaciones_integral_gr_281.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_281.gif)
![[Graphics:../Images/aplicaciones_integral_gr_282.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_282.gif)
La curva de ecuaciones paramétricas ![[Graphics:../Images/aplicaciones_integral_gr_305.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_305.gif) para
para ![[Graphics:../Images/aplicaciones_integral_gr_306.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_306.gif) es una cardioide. Es la curva que describe un punto fijo del borde de un círculo que rueda sin deslizar sobre otro del mismo radio.
es una cardioide. Es la curva que describe un punto fijo del borde de un círculo que rueda sin deslizar sobre otro del mismo radio.
![[Graphics:../Images/aplicaciones_integral_gr_307.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_307.gif)
![[Graphics:../Images/aplicaciones_integral_gr_308.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_308.gif)
La ecuación cartesiana de la cardioide es ![[Graphics:../Images/aplicaciones_integral_gr_309.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_309.gif) donde
donde ![[Graphics:../Images/aplicaciones_integral_gr_310.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_310.gif) es un parámetro positivo. Para ver cómo se genera la cardiode ejecuta la siguiente celda
es un parámetro positivo. Para ver cómo se genera la cardiode ejecuta la siguiente celda
![[Graphics:../Images/aplicaciones_integral_gr_311.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_311.gif)
![[Graphics:../Images/aplicaciones_integral_gr_312.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_312.gif)
![[Graphics:../Images/aplicaciones_integral_gr_334.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_334.gif)
![[Graphics:../Images/aplicaciones_integral_gr_335.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_335.gif)
La ecuación cartesiana de la lemniscata es ![[Graphics:../Images/aplicaciones_integral_gr_336.gif]](http://www.ugr.es/~dpto_am/docencia/cie_mat_calculo/aplicaciones_integral/Images/aplicaciones_integral_gr_336.gif) y se define como el lugar geométrico de los puntos del plano cuyo producto de distancias a dos puntos fijos es constante igual al cuadrado de la semidistancia entre dichos puntos. Observa que, a diferencia de las anteriores, la lemniscata no es una curva simple.
y se define como el lugar geométrico de los puntos del plano cuyo producto de distancias a dos puntos fijos es constante igual al cuadrado de la semidistancia entre dichos puntos. Observa que, a diferencia de las anteriores, la lemniscata no es una curva simple.
CURVAS POLARES
Por supuesto que existen muchísimas otras figuras que se forman a partir de las funciones en coordenadas polares, pero para este estudio se ha tratado de presentar las más importantes o comunes, a la vez que se muestra más de un ejemplo para casi todos los tipos de gráfico, de manera que resulte totalmente clara la forma que cada función tendrá al ser graficada en las coordenadas polares.
Se espera que al finalizar la lectura completa de este trabajo, se logre comprender claramente cada figura y se tenga una idea global de los tipos de gráfico que podemos desarrollar mediante funciones en coordenadas polares.


ROSA DE CUATRO HOJAS/PÉTALOS
Este tipo de gráfico se conoce como Rosa de cuatro pétalos. Es fácil ver cómo se forma una figura parecida a una rosa con cuatro pétalos. La función para este gráfico es:
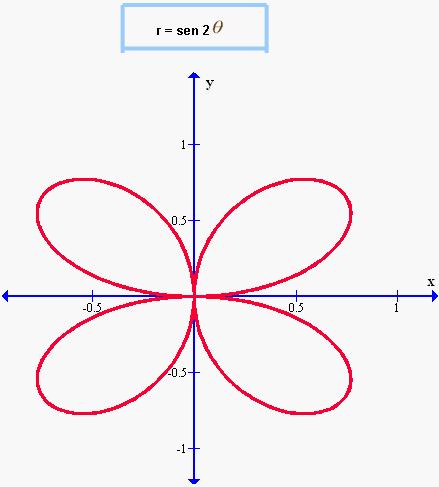
Presentamos ahora el gráfico llamado Rosa de tres pétalos. Analógicamente al gráfico de la rosa de cuatro pétalos, este gráfico es parecido pero tiene sólo tres hojas o pétalos en su forma gráfica. Un ejemplo es el siguiente:

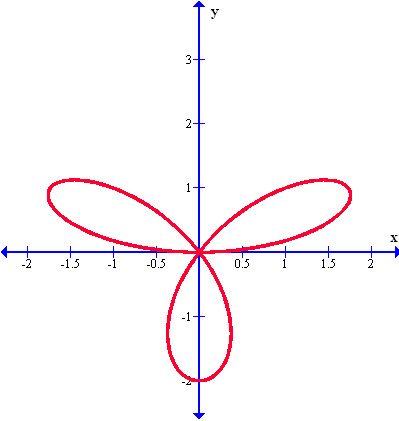
El siguiente gráfico es como los dos anteriores, pero ahora con ocho hojas o pétalos, tal como lo vemos en la siguiente función graficada:
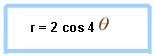
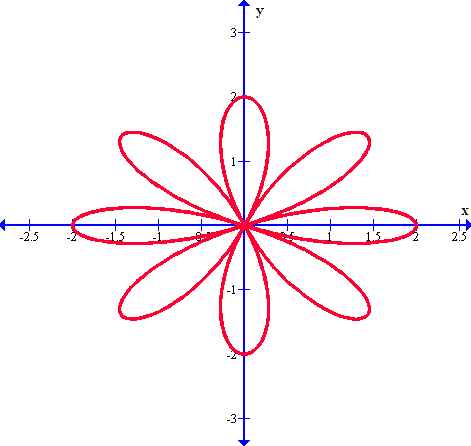
UNA ROSA DENTRO DE OTRA
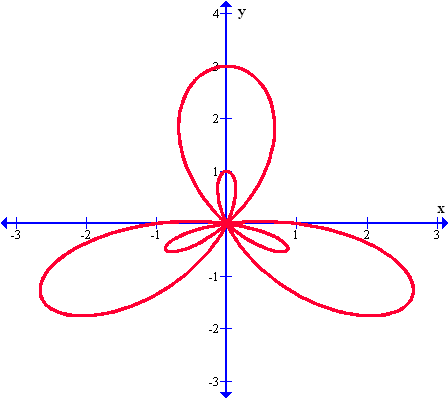
Un caso interesante y especial que se puede dar es el que se muestra en la gráfica que vemos a continuación, donde se aprecia una rosa de tres pétalos precisamente dentro de otra rosa de tres pétalos u hojas. Veamos:
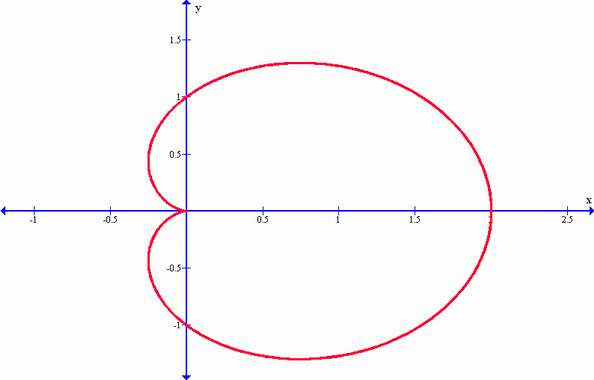
A continuación se presenta el tipo de gráfico que se denomina cardioide. Para este ejemplo se presenta una cardioide simétrica con respecto al eje poplar y que apunta hacia la derecha. Podemos observar que se distingue una figura como de un corazón, razón por la cual se llama este gráfico cardioide. La función que lo ha generado es:
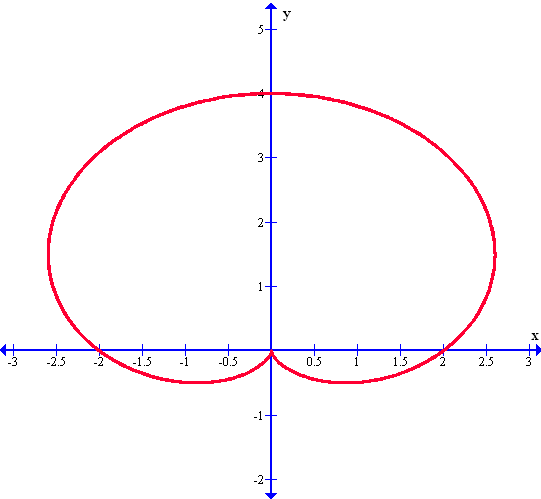
Habiendo visto el primer gráfico de una cardiode, se presenta otro gráfico de este tipo pero ahora apunta hacia arriba, tal como lo vemos a en el gráfico de la siguiente función:
LIMACONES O CARACOLES
Limaçon viene del latín limax que significa caracol. El caracol de Pascal, lo descubrió Etienne Pascal padre de Blaise Pascal en la primera mitad del siglo XVII y el nombre se lo dio Roberval en 1650 cuando la usó como ejemplo para mostrar su método para trazar tangentes. Un limaçon o las gráficaspolares que generan limaçones son las funciones en coordenadas polares con la forma:
r = 1 + b cos 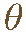
Ahora veamos un ejemplo concreto de un gráfico de este tipo, donde se muestra un caracol que apunta hacia la derecha y que tiene un lazo interior. La función para este gráfico es la siguiente:
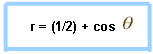
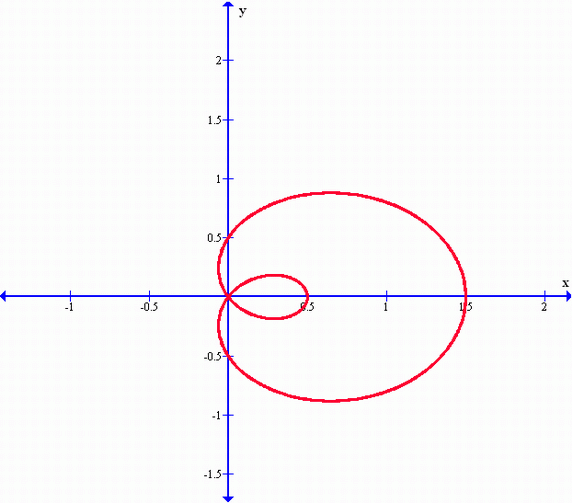
Veamos otro gráfico de una función que tiene como resultado un caracol con un lazo interior pero que a diferencia del gráfico anterior, este apunta hacia abajo. Veamos:
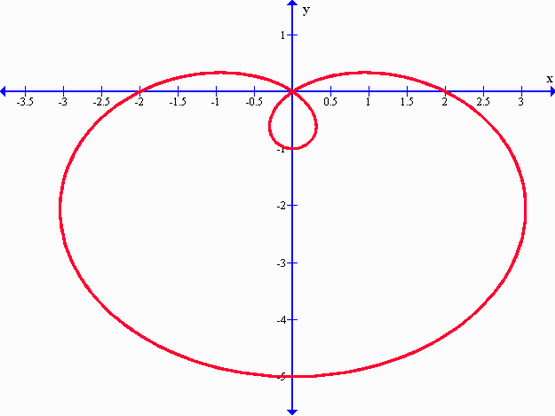
Continuando con la gráfica de caracoles o limacones, hay otro tipo que es el caracol con hendidura o caracol con concavidad. Como podremos observar, este no tiene lazo, y está dirigido hacia la izquierda. Veamos a continuación el gráfico que resulta, el cual apunta hacia la izquierda:
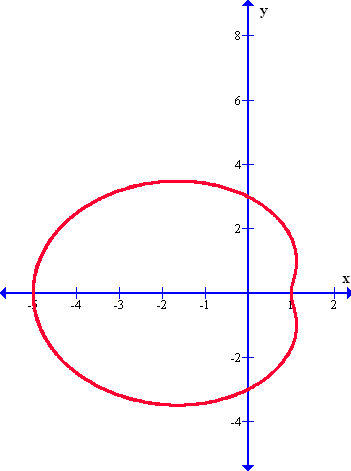
Ahora se muestra un gráfico igual al anterior con la diferencia que ahora está dirigido hacia la derecha, de modo que tenemos un limaçon o caracol con hendidura o concavidad que está dirigido hacia la derecha:
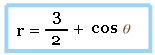
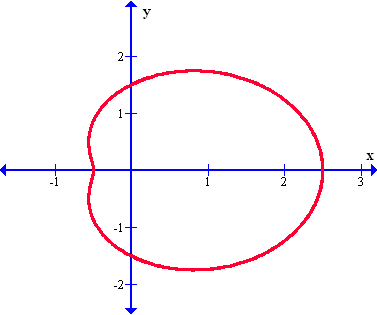
Antes de terminar el tema de los limacoides o caracoles, veamos otro gráfico diferente a los otros, que es conocido como caracol convexo o caracol ovalado, el cual está apuntando hacia arriba, como lo vemos en el gráfico siguiente:
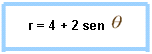
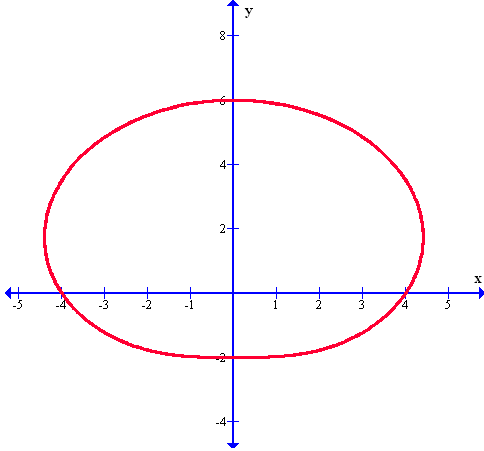
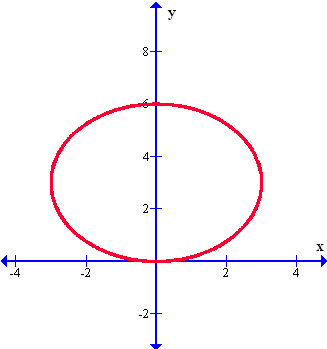
Esta nueva función nos presenta una forma conocida por todos y es precisamente la circunferencia, la cual será formada en el gráfico polar mediante la siguiente función:
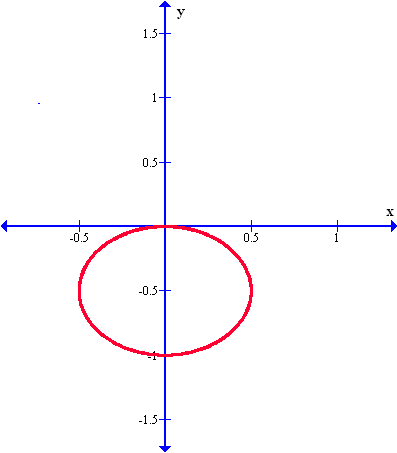
Ahora veamos una nueva gráfica que resulta en una circunferencia, con la única diferencia que ahora aparece arriba del rayo inicial (o del eje x que todos conocemos), a diferencia del gráfico anterior, que la circunferencia aparecía abajo del radio inicial. La función con su gráfico es esta:
LEMNISCATA
En matemáticas, una leminscata es un tipo de curva descrita por la siguiente ecuación en coordenadas polares:
La representación gráfica de esta ecuación genera una curva similar a 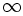 . La curva se ha convertido en el símbolo del infinito y es ampliamente utilizada en matemáticas. El símbolo en sí mismo es, a veces, llamado lemniscata. Un ejemplo de esta función con su respectivo gráfico lo apreciamos a continuación:
. La curva se ha convertido en el símbolo del infinito y es ampliamente utilizada en matemáticas. El símbolo en sí mismo es, a veces, llamado lemniscata. Un ejemplo de esta función con su respectivo gráfico lo apreciamos a continuación:
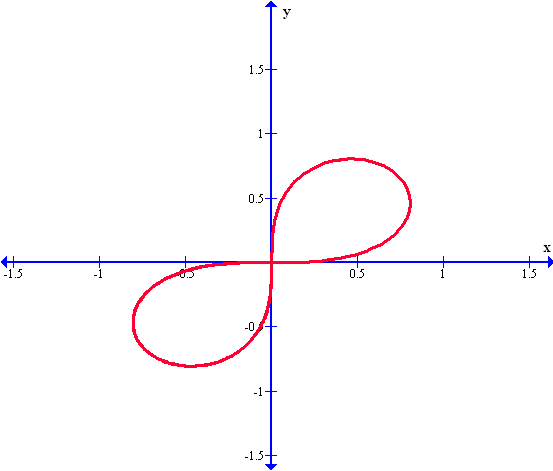
Tenemos otro ejemplo de lemniscata, pero ahora aparece a lo largo del eje x o en sentido horizontal:
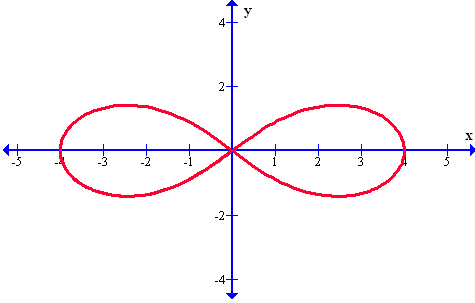
Finalmente se muestra un gráfico como los dos anteriores, donde aparece una lemniscata, con la única diferencia que ahora se muestra en sentido vertical.
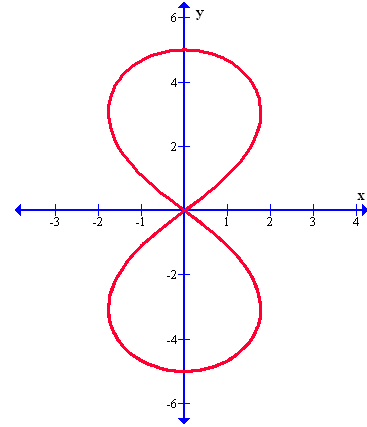
Esta es una curva muy reciente si hablamos relativamente a las demás. Hay curvas polares que tienen varios siglos de existir, mientras que esta que trataremos en este momento es bastante reciente, pues fue desarrollada por el matemático inglés T.J. Freeth, quien descubrió esta curva en 1879. Un ejemplo se aprecia en este gráfico:

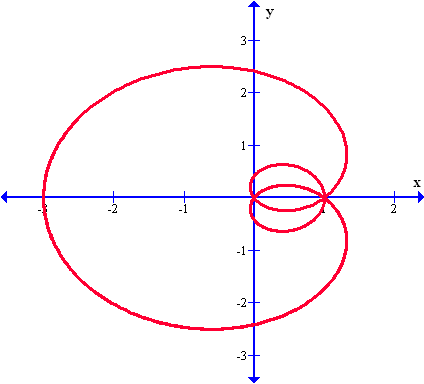
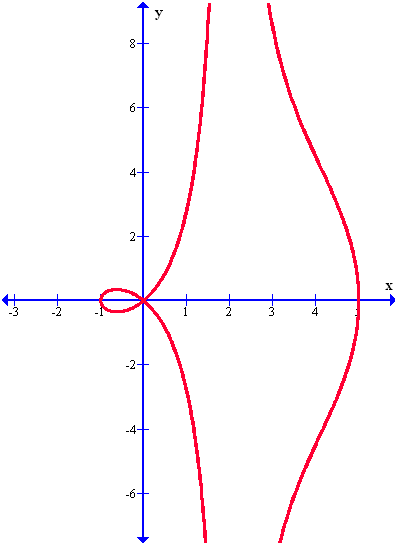
Nicómenes nació sobre el año 280 antes de Cristo en Grecia y murió en el año 210 a.C. Se sabe muy poco de su vida pero es famoso por su "Las líneas de la Concoide". Veamos un gráfico en coordenadas polares de la concoide de Nicómenes:
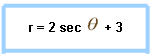
Suscribirse a:
Comentarios (Atom)