Blog Geogebra Crysta S: ¿Cómo convertir una curva paramétrica y polar a una rectangular o cartesiana?

POLARES

Es un sistema de coordendas bidimensional en el cual cada punto del plano se determina por un ángulo y una distancia.

De manera más precisa, se toman: un punto O del plano, al que se le llama origen o polo, y una recta dirigida (o rayo, o segmento OL) que pasa por O, llamada eje polar (equivalente al eje x del sistema cartesiano), como sistema de referencia. Con este sistema de referencia y una unidad de medida métrica (para poder asignar distancias entre cada par de puntos del plano), todo punto P del plano corresponde a un par ordenado (r, θ) donde r es la distancia de P al origen y θ es el ángulo formado entre el eje polar y la recta dirigida OP que va de O a P. El valor θ crece en sentido antihorario y decrece en sentido horario. La distancia r (r ≥ 0) se conoce como la «coordenada radial» o «radio vector», mientras que el ángulo es la «coordenada angular» o «ángulo polar».

En el caso del origen , O, el valor de r es cero, pero el valor de θ es indefinido. En ocasiones se adopta la convención de representar el origen por (0,0º).

En el plano de ejes xy con centro de coordenadas en el punto O se puede definir un sistema de coordenadas polares de un punto M del plano, definidas por la distancia r al centro de coordenadas, y el ángulo $\theta$ del vector de posición sobre el eje x. Conversión de coordenadas polares a rectangulares

Definido un punto en coordenadas polares por su ángulo $\theta$ sobre el eje x, y su distancia r al centro de coordenadas, se tiene:

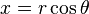
$x= r \cos \theta \,$

Conversión de coordenadas rectangulares a polares $y= r sen \theta \,$

Definido un punto del plano por sus coordenadas rectangulares (x,y), se tiene que la coordenada polar r es:

$r= \sqrt{x^2 +y^2}$ (aplicando el Teorema de Pitágoras)

Para determinar la coordenada angular θ, se deben distinguir dos casos:

Para $r$ = 0, el ángulo θ puede tomar cualquier valor real.
Para $r$ ≠ 0, para obtener un único valor de θ, debe limitarse a un intervalo de tamaño 2π. Por convención, los intervalos utilizados son [0, 2π) y (−π, π].

Para obtener θ en el intervalo [0, 2π), se deben usar las siguientes fórmulas ( $\arctan$ denota la inversa de la función tangente):

$\theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{si } x > 0 \mbox{ y } y \ge 0\\ \arctan(\frac{y}{x}) + 2\pi & \mbox{si } x > 0 \mbox{ y } y < 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{si } x < 0\\ \frac{\pi}{2} & \mbox{si } x = 0 \mbox{ y } y > 0\\ \frac{3\pi}{2} & \mbox{si } x = 0 \mbox{ y } y < 0 \end{cases}$

Para obtener θ en el intervalo (−π, π], se deben usar las siguientes fórmulas:

$\theta = \begin{cases} 2\arctan(\frac{y}{x + |z|}) & \mbox{si } x \not\in \Bbb R^-\\ \pi & \mbox{si } x \in \Bbb R^- \\ \end{cases}$

o equivalentemente

$\theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{si } x > 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{si } x < 0 \mbox{ y } y \ge 0\\ \arctan(\frac{y}{x}) - \pi & \mbox{si } x < 0 \mbox{ y } y < 0\\ \frac{\pi}{2} & \mbox{si } x = 0 \mbox{ y } y > 0\\ -\frac{\pi}{2} & \mbox{si } x = 0 \mbox{ y } y < 0 \end{cases}$

Muchos lenguajes de programación modernos evitan tener que almacenar el signo del numerador y del denominador gracias a la implementación de la función atan2, que tiene argumentos separados para el numerador y el denominador. En los lenguajes que permiten argumentos opcionales, la función atan puede recibir como parámetro la coordenada x.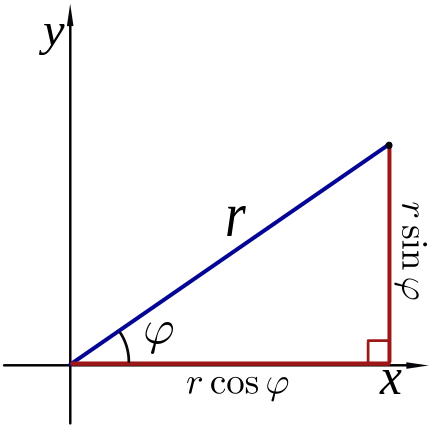

PARAMÉTRICAS

Hallar la gráfica de la ecuación cartesiana y dominio de las funciones dadas por sus ecuaciones paramétricas. Indicar el movimiento.
a) $\begin{Bmatrix} x(t)= t+1& \mbox{ }& \\y(t)=t^2+1 & \mbox{}&\end{matrix}$ con $t \in{[0,1]}$

b) $\begin{Bmatrix} x(t)= 2\sen^2{t}& \mbox{ }& \\y(t)=2\cos^2{t} & \mbox{}&\end{matrix} t \in {[0,2 \pi]}$

c) $\begin{Bmatrix} x(t)= -cos{t}& \mbox{ }& \\y(t)=sen{t} & \mbox{}&\end{matrix} t \in{[\displaystyle\frac{ \pi}{2},\displaystyle\frac{3}{2} \pi]}$

Encontrar un representación parametrica de:
a)

Un cambio útil suele ser:
(*):Si

es una función (con el debido abuso de notación), entonces siempre se puede parametrizar a la curva como

(**):A demás, hay que aprender a reconocer curvas. Por ejemplo, las circunferencias centradas en el origen con radio

siempre son de la forma $r(\theta)=(rcos(a\theta),rsin(a\theta))$ con $\theta\in{[0,2\pi/a}$ , $a\neq{0}$ .

Usando lo anterior, los dos incisos (a), el segundo (b) y casi el (c).

Por ejemplo, para el primer (a) se tiene: llamando