GeoGebra opera con dos tipos de curvas, paramétricas o implícitas.
Curvas Paramétricas
- Estas curvas pueden...
- vincularse a comandos como Tangente o Punto y, en GeoGebra 4.2 a Comando Interseca
- complementarse con empleo de herramientas como
Nuevo Punto y Tangente para , por ejemplo, trazar una tangente por un punto de la curva - asociarse a expresiones aritméticas o funciones predefinidas. Por ejemplo,
c(3)brinda el punto de posición paramétrica 3 en la curva c. - tantearse. Al tratar con extremos, digamos a y b, dinámicos se puede apelar también a deslizadores variables.Nota: Ver la
herramienta Deslizador.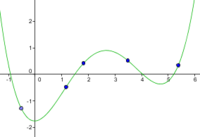
POLARES
Para graficar en coordenadas polares con GeoGebra se procede de la siguiente forma:
Sabemos que la sintaxis para graficar un punto en este programa es (x, y), bien pues para poner un punto en coordenadas polares r, theta la sintaxis es (r; theta); aquí emplearemos punto y coma para que se trate de coordenadas polares.
Ahora, si quieres dibujar el plano polar escribiremos el siguiente código:
Primero:
Secuencia[Circunferencia[(0,0), i], i,1,10]
Esto crea una secuencia o familia de círculos de centro en el origen con un incremento de 1 y con 10 círculos en total (esto lo puedes variar).
Segundo:
Secuencia[Recta[(0,0),(cos(i),sin(i))],i,0,2pi,pi/6]
Esto crea una familia de rectas que pasan por el origen con un incremento en el ángulo de inclinación de pi/6
Con esto ya tienes tu plano polar, ahora para dibujar curvas polares vamos a tener que parametrizar las funciones de la siguiente manera:
Primero ingresamos la función; por ejemplo r(x)=cos(2*x), la graficamos y luego la ocultamos (donde dice mostrar objeto), a continuación escribimos el siguiente código:
Curva[r(t)*cos(t), r(t)*sin(t), t, 0, 2pi]
y ya con esto tienes la grafica de una curva polar.
Y esta es la forma, o por lo menos una de las formas, de trabajar con gráficas y curvas en el plano polar con GeoGebra.
Sabemos que la sintaxis para graficar un punto en este programa es (x, y), bien pues para poner un punto en coordenadas polares r, theta la sintaxis es (r; theta); aquí emplearemos punto y coma para que se trate de coordenadas polares.
Ahora, si quieres dibujar el plano polar escribiremos el siguiente código:
Primero:
Secuencia[Circunferencia[(0,0), i], i,1,10]
Esto crea una secuencia o familia de círculos de centro en el origen con un incremento de 1 y con 10 círculos en total (esto lo puedes variar).
Segundo:
Secuencia[Recta[(0,0),(cos(i),sin(i))],i,0,2pi,pi/6]
Esto crea una familia de rectas que pasan por el origen con un incremento en el ángulo de inclinación de pi/6
Con esto ya tienes tu plano polar, ahora para dibujar curvas polares vamos a tener que parametrizar las funciones de la siguiente manera:
Primero ingresamos la función; por ejemplo r(x)=cos(2*x), la graficamos y luego la ocultamos (donde dice mostrar objeto), a continuación escribimos el siguiente código:
Curva[r(t)*cos(t), r(t)*sin(t), t, 0, 2pi]
y ya con esto tienes la grafica de una curva polar.
Y esta es la forma, o por lo menos una de las formas, de trabajar con gráficas y curvas en el plano polar con GeoGebra.
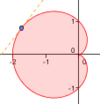
MUY BUEN TRABAJO CRUSTAL.?PERO COMO GRAFICAR EL AREA DEMTRO DE LA CUTVA PARAMETRICA O POLAR..HACIENDOLO A LAPIZ ESTO YA LO SE.PERO EN GEOGEBRA COMO SE GRAFICA DICHA AREA.PQ NO VEO EN LOS VIDEOS COMO SE RESUELVE.SE DE LA INTEGRAL DE UNA FUNCION MAS NO LA DE LA PARAMETRICA.!FELICITACIONES!
ResponderEliminar