MÉTODOS DE SOLUCIÓN DE ECUACIONES
1. MÉTODO DE NEWTON-RAPHSON
En análisis numérico, el método de Newton (conocido también como el método de Newton-Raphson o el método de Newton-Fourier) es un algoritmo eficiente para encontrar aproximaciones de los ceros o raíces de una función real. También puede ser usado para encontrar el máximo o mínimo de una función, encontrando los ceros de su primera derivada
El método de Newton-Raphson es un método abierto, en el sentido de que su convergencia global no está garantizada. La única manera de alcanzar la convergencia es seleccionar un valor inicial lo suficientemente cercano a la raíz buscada. Así, se ha de comenzar la iteración con un valor razonablemente cercano al cero (denominado punto de arranque o valor supuesto). La relativa cercanía del punto inicial a la raíz depende mucho de la naturaleza de la propia función; si ésta presenta múltiples puntos de inflexión o pendientes grandes en el entorno de la raíz, entonces las probabilidades de que el algoritmo diverja aumentan, lo cual exige seleccionar un valor supuesto cercano a la raíz. Una vez que se ha hecho esto, el método linealiza la función por la recta tangente en ese valor supuesto. La abscisa en el origen de dicha recta será, según el método, una mejor aproximación de la raíz que el valor anterior. Se realizarán sucesivas iteraciones hasta que el método haya convergido lo suficiente. f'(x)= 0 Sea f : [a, b] -> R función derivable definida en el intervalo real [a,b]. Empezamos con un valor inicial x0 y definimos para cada número natural n
Donde f ' denota la derivada de f.
Nótese que el método descrito es de aplicación exclusiva para funciones de una sola variable con forma analítica o implícita conocible. Existen variantes del método aplicables a sistemas discretos que permiten estimar las raíces de la tendencia, así como algoritmos que extienden el método de Newton a sistemas multivariables, sistemas de ecuaciones, etc.
PROCEDIMIENTO
Suponga que se desea minimizar la función f(x) con n variables y que ´esta se aproxima utilizando el
desarrollo de Taylor hasta orden. Así f(x) ≈ φ(x) = f(xo) + (x − xo)′∇f(xo) + 1
2(x − xo)′Hf(xo) (x − xo)
Si la aproximaxión de f(x) por φ(x) es buena, un mínimo relativo f(x) se podría aproximar por un mínimo
relativo de por φ(x). Supongamos que x1 es un mínimo relativo de φ(x), entonces x1 es un punto estacionario para φ(x), as´ı ∇φ(x1) = 0. Desarrollando el gradiente de φ(x), sustituyendo x1 por x e igualando a 0 tenemos:
∇f(xo) + Hf(xo)(x1 − x0) = 0
Si la matriz hessiana Hf(xo) es invertible tenemos quex1 = xo − Hf−1(xo)∇f(xo) (1)
La expresión anterior se usa como una ecuación de recurrencia para dado un punto inicial generar una suceción de puntos que deben converger al mínimo local de f(x). Como calcular la inversa de una matriz tiene una mayor complejidad (8/3 n3) que resolver un sistema de ecuaciones (2/3 n3), la expresi´on Hf−1(xo)∇f(xo) se obtieneresolviendo el sistema[Hf(xo)|∇f(xo)].
OBTENCIÓN DE LA FORMULA
El Método de Newton tiene una interpretación geométrica sencilla, de hecho, el Método de Newton consiste en una linealización de la función, es decir, f se reemplaza por una recta tal que contiene al punto (xo, f (xo)) y cuya pendiente coincide con la derivada de la función en el punto, f (xo) . La nueva aproximación a la raíz, x1 , se obtiene de la intersección de la función lineal con el eje X de ordenadas.
La ecuación de la recta que pasa por el punto (xo, f (xo)) y de la pendiente f ‘(xo) es :
y- f (xo) = f ‘(xo)(x-xo) .
De donde, haciendo y=0 y despejando x se obtiene la ecuación de Newton- Raphson.
Xn+1 = Xn – f (Xn) / f ‘(xn)

Demostración: Sea 0 x la raíz supuesta inicial o valor inicial de las iteraciones y si se aplican funciones trigonométricas al ángulo α de la figura 4 se tiene que tan(α ) = f (xo) /(xo − x1) , a partir de esta fórmula se puede decir que: (x0 − x1) = f (x0 ) / tan(α ) . y despejando x1 se tendría la fórmula de Newton. La pendiente en xo esta dada por tan(α ) = f ‘(xo) . Teniendo en cuenta lo anterior se tendría entonces que: x1 = x0 − f (xo) / f ‘(xo ) .
También se puede deducir de teniendo en cuenta que la ecuación de la línea tangente en xo esta dada por y- f (xo) = f ‘(xo)(x-xo) . La primera aproximación x1 es
Obtenida como la raíz de (1). Así (x1,0) es un punto sobre la ecuación anterior.
Donde, Xn una valor para x conocido actualmente, f(Xn) representa el valor de la función evaluada en Xn , y f’(Xn) es la derivada evaluada en Xn, Xn+1 representa el próximo valor para x que se está tratando de encontrar como raíz al aplicar el modelo. Esencialmente, f’(X0) , la derivada representa f(x)/dx , (dx = delta-x) ó dx = X1- X0 . Sin embargo, el término f (x) / f `(x) representa un valor de dx = Δx .
EJEMPLO
Solución:
En este caso, tenemos que
 |
De aquí tenemos que:
 |
Comenzamos con Xo= l y obtenemos:
 |
En este caso, el error aproximado es,
 |
Continuamos el proceso hasta reducir el error aproximado hasta donde se pidió.
Resumimos los resultados en la siguiente tabla:
Resumimos los resultados en la siguiente tabla:
Aprox. a la raíz
| Error aprox. |
| 1 | |
| 1.268941421 | 21.19% |
| 1.309108403 |
3.06%
|
| 1.309799389 |
0.052%
|
Observe que cuando el método de Newton-Raphson converge a la raíz, lo hace de una forma muy rápida y de hecho, observamos que el error aproximado disminuye a pasos agigantados en cada paso del proceso. Aunque no es nuestro objetivo establecer formalmente las cotas para los errores en cada uno de los métodos que hemos estudiado, cabe mencionar que si existen estas cotas que miden con mayor precisión la rapidez ó lentitud del método en estudio.
2. MÉTODO DE BISECCIÓN

El método de bisección se basa en el siguiente teorema de Cálculo:
Sea 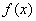 contínua en un intervalo
contínua en un intervalo 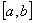 y supongamos que
y supongamos que 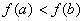 . Entonces para cada
. Entonces para cada 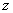 tal que
tal que 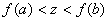 , existe un
, existe un 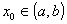 tal que
tal que 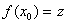 . La misma conclusión se obtiene para el caso que
. La misma conclusión se obtiene para el caso que 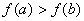 .
.
Básicamente el Teorema del Valor Intermedio nos dice que toda función contínua en un intervalo cerrado, una vez que alcanzó ciertos valores en los extremos del intervalo, entonces debe alcanzar todos los valores intermedios.
En particular, si 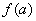 y
y 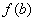 tienen signos opuestos, entonces un valor intermedio es precisamente
tienen signos opuestos, entonces un valor intermedio es precisamente 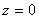 , y por lo tanto, el Teorema del Valor Intermedio nos asegura que debe existir
, y por lo tanto, el Teorema del Valor Intermedio nos asegura que debe existir 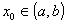 tal que
tal que 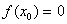 , es decir, debe haber por lo menos una raíz de
, es decir, debe haber por lo menos una raíz de 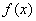 en el intervalo
en el intervalo 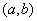 .
.
El método de bisección sigue los siguientes pasos:
Sea 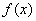 contínua,
contínua,
i) Encontrar valores iniciales 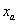 ,
, 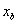 tales que
tales que 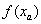 y
y 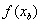 tienen signos opuestos, es decir,
tienen signos opuestos, es decir,
ii) La primera aproximación a la raíz se toma igual al punto medio entre 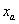 y
y 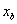 :
:
iii) Evaluar 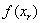 . Forzosamente debemos caer en uno de los siguientes casos:
. Forzosamente debemos caer en uno de los siguientes casos:
En este caso, tenemos que 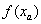 y
y 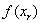 tienen signos opuestos, y por lo tanto la raíz se encuentra en el intervalo
tienen signos opuestos, y por lo tanto la raíz se encuentra en el intervalo 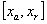 .
.
En este caso, tenemos que 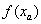 y
y 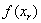 tienen el mismo signo, y de aquí que
tienen el mismo signo, y de aquí que 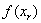 y
y 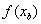 tienen signos opuestos. Por lo tanto, la raíz se encuentra en el intervalo
tienen signos opuestos. Por lo tanto, la raíz se encuentra en el intervalo 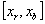 .
.
En este caso se tiene que 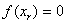 y por lo tanto ya localizamos la raíz.
y por lo tanto ya localizamos la raíz.
El proceso se vuelve a repetir con el nuevo intervalo, hasta que:
es decir,
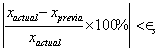 |
EJEMPLO
Aproximar la raíz de 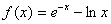 hasta que
hasta que 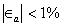 .
.
Solución
En efecto, tenemos que
mientras que
Cabe mencionar que la función 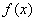 sí es contínua en el intervalo
sí es contínua en el intervalo 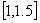 . Así pues, tenemos todos los requisitos satisfechos para poder aplicar el método de bisección. Comenzamos:
. Así pues, tenemos todos los requisitos satisfechos para poder aplicar el método de bisección. Comenzamos:
i) Calculamos el punto medio (que es de hecho nuestra primera aproximación a la raíz):
ii) Evaluamos 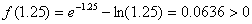
iii) Para identificar mejor en que nuevo intervalo se encuentra la raíz, hacemos la siguiente tabla:
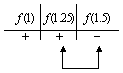
Por lo tanto, vemos que la raíz se encuentra en el intervalo 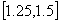 .
.
En este punto, vemos que todavía no podemos calcular ningún error aproximado, puesto que solamente tenemos la primera aproximación. Así, repetimos el proceso con el nuevo intervalo 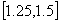 .
.
Calculamos el punto medio (que es nuestra segunda aproximación a la raíz):
Aquí podemos calcular el primer error aproximado, puesto que contamos ya con la aproximación actual y la aproximación previa:
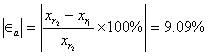 |
Puesto que no se ha logrado el objetivo, continuamos con el proceso.
Evaluamos 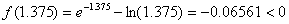 , y hacemos la tabla:
, y hacemos la tabla:
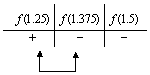
Así, vemos que la raíz se encuentra en el intervalo 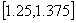 .
.
Calculamos el punto medio,
Y calculamos el nuevo error aproximado:
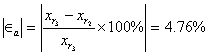 |
El proceso debe seguirse hasta cumplir el objetivo.
Resumimos los resultados que se obtienen en la siguiente tabla:
Aprox. a la raíz | Error aprox. |
| 1.25 | |
| 1.375 | 9.09% |
| 1.3125 | 4.76% |
| 1.28125 | 2.43% |
| 1.296875 | 1.20% |
| 1.3046875 | 0.59% |
| Así, obtenemos como aproximación a la raíz |
Ejemplo 2
Aproximar la raíz de  hasta que
hasta que 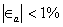 .
.
Solución
Como vimos en el ejemplo 2 de la sección anterior, la única raíz de 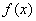 se localiza en el intervalo
se localiza en el intervalo 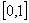 . Para poder aplicar el método de bisección, es importante checar que sí se cumplen las hipótesis requeridas.
. Para poder aplicar el método de bisección, es importante checar que sí se cumplen las hipótesis requeridas.
Sabemos que 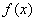 es contínua en el intervalo
es contínua en el intervalo 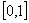 , y checamos que
, y checamos que 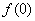 y
y 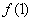 tengan signos opuestos.
tengan signos opuestos.
En efecto,
Mientras que,
Por lo tanto, sí podemos aplicar el método de bisección.
Calculamos el punto medio del intervalo 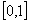 ,
,
Que es la primera aproximación a la raíz de 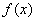 .
.
Evaluamos 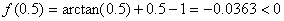 .
.
Y hacemos nuestra tabla de signos,
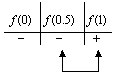
Puesto que 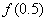 y
y 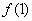 tienen signos opuestos, entonces la raíz se localiza en el intervalo
tienen signos opuestos, entonces la raíz se localiza en el intervalo 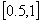 .
.
En este punto, solo contamos con una aproximación, a saber, 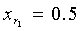 , que es el primer punto medio calculado.
, que es el primer punto medio calculado.
Repetimos el proceso, es decir, calculamos el punto medio ahora del intervalo 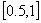 ,
,
Que es la nueva aproximación a la raíz de 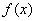 .
.
Aquí podemos calcular el primer error aproximado:
Puesto que no se cumple el objetivo, continuamos con el proceso.
Evaluamos 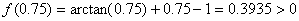 .
.
Y hacemos la tabla de signos:
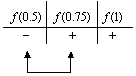
Puesto que 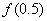 y
y 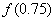 tienen signos opuestos, entonces la raíz se localiza en el intervalo
tienen signos opuestos, entonces la raíz se localiza en el intervalo 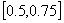 .
.
Calculamos el punto medio,
Y el nuevo error aproximado:
El proceso se debe continuar hasta que se logre el objetivo.
Resumimos los resultados que se obtienen en la siguiente tabla:
Aprox. a la raíz | Error aprox. |
| 0.5 | |
| 0.75 | 33.33% |
| 0.625 | 20% |
| 0.5625 | 11.11% |
| 0.53125 | 5.88% |
| 0.515625 | 3.03% |
| 0.5234375 | 1.49% |
| 0.51953125 | 0.75% |
De lo cual, vemos que la aproximación buscada es 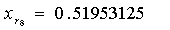
El método de bisección por lo general es lento, y en casos como el de la siguiente gráfica, puede ser demasiado lento.
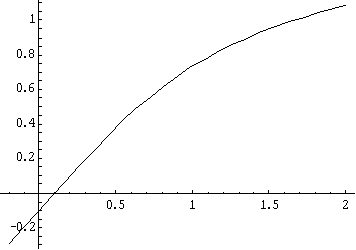 |
En un caso como éste, el proceso de bisección comienza a acercarse a la raíz de forma muy lenta, ya que el método solamente toma en cuenta que la raíz se encuentra dentro del intervalo, sin importar si se encuentra más cerca de alguno de los extremos del intervalo. Sería bueno implementar un método que tome en cuenta este detalle.
3. MÉTODO FALSA POSICIÓN
Método de regula falsi (regla falsa) o falsa posición es un método iterativo que a diferencia del método de la bisección, este se basa en una visualización grafica que consiste en unir f(a0) y f(b0) con una línea recta, la intersección de esta recta con el eje de coordenadas x representa una mejor aproximación de la raíz que por el método de la bisección, aunque no siempre es así.
Hallaremos la pendiente de la grafica de la recta trazada entre los puntos (a,f(a)) y (b,f(b)), donde la intersección con el eje de abscisas o línea horizontal sera nuestra aproximación a la raíz xi .
Podremos notar que la regula falsi determina el promedio ponderado de los extremos del intervalo.
Algoritmo de la falsa posición
Paso 1: dada la ecuación f(x)=0 ubicar el intervalo donde exista la raíz r є [a , b]
Paso 2: generar la sucesión {xi} con la siguiente relación.
Paso 3:
Determinar
Paso 4: si |x-x|≤ є dejar de iterar, caso contrario ir al paso 2
EJEMPLO
Sea la función donde x є [0,3] resolver por el método de falsa posición
- ¿Cuántas cifras significativas tiene la solución en la cuarta iteración?
- ¿Cuántas cifras decimales tiene la solución en la cuarta iteración?
Solución
Primero buscamos el intervalo donde podemos encontrar al menos una raíz.
f(0).f(1) < 0 entonces el intervalo a trabajar será [0,1]
Iteración inicial
Primera iteración
Segunda iteración
Tercera iteración
Cuarta iteración
Respondiendo a las preguntas planteadas
2.
4. MÉTODO DEL PUNTO FIJO
Un punto fijo de una función  , es un número
, es un número  tal que
tal que  . El problema de encontrar las soluciones de una ecuación
. El problema de encontrar las soluciones de una ecuación  y el de encontrar los puntos fijos de una función
y el de encontrar los puntos fijos de una función  son equivalentes en el siguiente sentido: dado el problema de encontar las soluciones de una ecuación
son equivalentes en el siguiente sentido: dado el problema de encontar las soluciones de una ecuación  , podemos definir una función
, podemos definir una función  con un punto fijo
con un punto fijo  de muchas formas; por ejemplo,
de muchas formas; por ejemplo,  . En forma inversa, si la función
. En forma inversa, si la función  tiene un punto fijo en
tiene un punto fijo en  , entonces la función definida por
, entonces la función definida por  posee un cero en
posee un cero en  .
.
El método de punto fijo inicia con una aproximación inicial  y
y  genera una sucesión de aproximaciones la cual converge a la solución de la ecuación
genera una sucesión de aproximaciones la cual converge a la solución de la ecuación  . A la función
. A la función  se le conoce como función iteradora. Se puede demostrar que dicha sucesión
se le conoce como función iteradora. Se puede demostrar que dicha sucesión  converge siempre y cuando
converge siempre y cuando  .
.
Ejemplo
Usando el método de punto fijo vamos a aproximar la solución de la ecuación  dentro del intervalo
dentro del intervalo ![$ [1,2]$](http://www.tec-digital.itcr.ac.cr/revistamatematica/HERRAmInternet/ecuaexecl/ImagenesTexto/img179.gif) .
.
Lo primero es buscar una función  adecuada
adecuada
| 0 | |||
 |
Y claramente elegimos como función iteradora a

además observe que

para toda ![$ x \in [1,2]$](http://www.tec-digital.itcr.ac.cr/revistamatematica/HERRAmInternet/ecuaexecl/ImagenesTexto/img187.gif) , lo cual garantiza que la sucesión que vamos a construir va a ser convergente.
, lo cual garantiza que la sucesión que vamos a construir va a ser convergente.
La implementación de este método en Excel es realmente simple, como veremos.
|
5. MÉTODO DE LA SECANTE
Este método se basa en la fórmula de newton-raphson, pero evita el cálculo de la derivada usando la siguiente aproximación:
sustituyendo en la fórmula de newton-raphson, obtenemos:
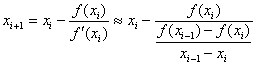
que es la fórmula del método de la secante. nótese que para poder calcular el valor de 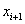 , necesitamos conocer los dos valores anteriores
, necesitamos conocer los dos valores anteriores 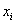 y
y 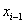 .
.
obsérvese tambien, el gran parecido con la fórmula del método de la regla falsa. la diferencia entre una y otra es que mientras el método de la regla falsa trabaja sobre intervalos cerrados, el método de la secante es un proceso iterativo y por lo mismo, encuentra la aproximación casi con la misma rapidez que el método de newton-raphson. claro, corre el mismo riesgo de éste último de no converger a la raíz, mientras que el método de la regla falsa va a la segura.
ejemplo 1
usar el método de la secante para aproximar la raíz de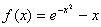 , comenzando con
, comenzando con 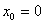 ,
, 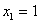 y hasta que
y hasta que 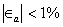 .
.
usar el método de la secante para aproximar la raíz de
solución
tenemos que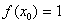 y
y 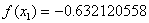 , que sustituímos en la fórmula de la secante para calcular la aproximación
, que sustituímos en la fórmula de la secante para calcular la aproximación 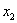 :
:
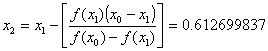
tenemos que
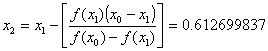
con un error aproximado de:
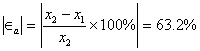
como todavía no se logra el objetivo, continuamos con el proceso. resumimos los resultados en la siguiente tabla:
aprox. a la raíz
|
error aprox.
|
0
| |
1
|
100%
|
0.612699837
|
63.2%
|
0.653442133
|
6.23%
|
0.652917265
|
0.08%
|
de lo cual concluímos que la aproximación a la raíz es:
EJEMPLOusar el método de la secante para aproximar la raíz de  , comenzando con
, comenzando con 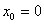 y
y 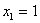 , y hasta que
, y hasta que 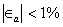 .
.
solución
tenemos los valores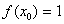 y
y 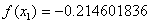 , que sustituímos en la fórmula de la secante para obtener la aproximación
, que sustituímos en la fórmula de la secante para obtener la aproximación 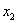 :
:
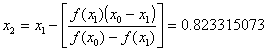
tenemos los valores
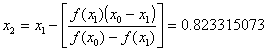
con un error aproximado de:
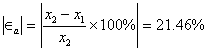
como todavía no se logra el objetivo, continuamos con el proceso. resumimos los resultados en la siguiente tabla:
aprox. a la raíz
|
error aprox.
|
0
| |
1
|
100%
|
0.823315073
|
21.4%
|
0.852330280
|
3.40%
|
0.853169121
|
0.09%
|
de lo cual concluímos que la aproximación a la raíz es:
Ejemplo 1
Usar el método de la secante para aproximar la raíz de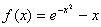 , comenzando con
, comenzando con 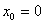 ,
, 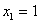 y hasta que
y hasta que 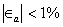 .
.
Usar el método de la secante para aproximar la raíz de
Solución
Tenemos que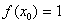 y
y 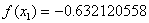 , que sustituímos en la fórmula de la secante para calcular la aproximación
, que sustituímos en la fórmula de la secante para calcular la aproximación 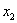 :
:
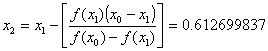
Tenemos que
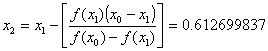
Con un error aproximado de:
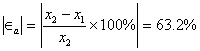
Como todavía no se logra el objetivo, continuamos con el proceso. Resumimos los resultados en la siguiente tabla:
| Aprox. a la raíz |
Error aprox.
|
| 0 | |
| 1 | 100% |
| 0.612699837 | 63.2% |
| 0.653442133 | 6.23% |
| 0.652917265 | 0.08% |
De lo cual concluímos que la aproximación a la raíz es:
Ejemplo 2Usar el método de la secante para aproximar la raíz de
Solución
Tenemos los valores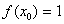 y
y 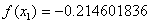 , que sustituímos en la fórmula de la secante para obtener la aproximación
, que sustituímos en la fórmula de la secante para obtener la aproximación 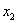 :
:
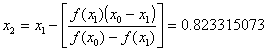
Tenemos los valores
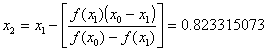
Con un error aproximado de:
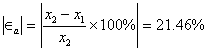
Como todavía no se logra el objetivo, continuamos con el proceso. Resumimos los resultados en la siguiente tabla:
| Aprox. a la raíz |
Error aprox.
|
| 0 | |
| 1 | 100% |
| 0.823315073 | 21.4% |
| 0.852330280 | 3.40% |
| 0.853169121 | 0.09% |
De lo cual concluímos que la aproximación a la raíz es:
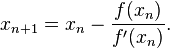





























No hay comentarios:
Publicar un comentario